DWA path planning algorithm
本文介绍了关于动态窗口算法(Dynamic Window Approaches, DWA)的一些基本概念与算法步骤。
基本概念
动态窗口算法(Dynamic Window Approaches, DWA),核心思想是根据无人设备当前的位置状态和速度状态在速度空间 (v,ω) 中确定一个满足无人设备硬件约束的采样速度空间,然后计算无人设备在这些速度情况下移动一定时间内的轨迹,并通过评价函数对该轨迹进行评价,最后选出评价最优的轨迹所对应的速度作为无人设备运动速度,如此循环直至移动无人设备到达目标点。
系统设计过程中对动态窗口算法的实现主要从三个方面出发,速度采样、轨迹预测、轨迹评价。
速度采样
现实中不同型号的无人设备所具有的硬件和结构不同,在物理层面上存在一定的限制,例如马力和重量会导致其最大加速度和最大转向加速度受到限制,反映在运动上的限制是运行速度的改变和方向变换的及时性。
在系统的仿真模拟中,不同模型的无人船也会设置不同的加速度参数,动态窗口算法的速度采样空间Vs会收到约束。
速度范围约束:由于真实环境中阻力等物理因素的存在,针对无人船进行建模时根据它的型号对线速度和角速度范围进行了限制,v∈[vmin ,vmax ],ω∈[ωmin ,ωmax ]。在此条件下可采样的速度空间Vm的限定范围:
$$ {V}_m=\lbrace(v,ω)∣v∈[v_{min} ,v_{max} ],ω∈[ω_{min} ,ω_{max} ]\rbrace $$加速度约束:针对某一时间点,忽略加速度变化所需时间,线加速度和角加速度的范围被约束在av∈[-avmax ,avmax],aω∈[-aωmax ,aωmax],假定vc、ωc 分别为无人船当前时刻的线速度和角速度,在极短的时间Δt内,可采样的速度空间Vd也被限定:
$$ {V}_d=\lbrace(v,ω)∣v∈[v_c−a_{vmax}⋅Δt,v_c+a_{vmax}·Δt], ω∈[ω_c−a_{ωmax}·Δt,ω_c+a_{ωmax}·Δt]\rbrace $$障碍物安全距离约束:当无人船与障碍物之间的距离缩小到达一定程度时,此时即使采用最大加速度进行减速,也无法避免的发生碰撞,基于此对速度采样空间也进行了限制:
$$ {V}_a=\lbrace(v,ω)∣v∈[v_{min} ,2·dist·a_{vmax} ],ω∈[ω_{min} ,2·dist·a_{ωmax} ]\rbrace $$其中,dist表示当前无人设备的位置与障碍物的最近距离。综合以上三个速度空间的限制,通过取交集获取最终的速度采样空间,即:
$$ V_s=V_m∩V_d∩V_a $$轨迹预测
在完成了速度采样空间Vs的确认之后,根据动态窗口算法设置的采样率来对采样空间进行拆分组合。分别用Ev和Ew表示表示线速度和角速度的采样频率,即每间隔Ev进行一次速度采样,根据排列组合能够组成的线速度与角速度组数:
$$ n=[(v_{high}−v_{low})/E_v]⋅[(w_{high}−w_{low})/E_w] $$每一组(v,ω)按照设置的无人船运动模型,计算其在设置的预测时间内运动轨迹并保存,系统采用的运动模型是差分驱动模型:
$$ \left\{ \begin{aligned} x_k & = x_{k−1}+v⋅\cos(θ_{k−1})Δt \\ y_k & = y_{k−1}+v⋅\sin(θ_{k−1})Δt \\ θ_k & = θ_{k-1}+ωΔt \end{aligned} \right. $$其中,(x,y,θ)代表无人船的位置状态,k代表采样时刻,Δt代表采样间隔。
轨迹评价
经过轨迹预测后得到的n组轨迹,需要经过评价函数来选择最优的轨迹作为无人船接下来的运动轨迹。轨迹评价考虑三个方面:方位角评价,评估轨迹末端位置方向与目标点连线的夹角误差,引导无人船朝向目标;距离评价,计算当前速度下轨迹与障碍物之间的最近距离,避免无人船与障碍物发生碰撞;速度评价,表示当前的速度大小,鼓励无人船保持较高的速度以提高导航效率。
评价函数量化表现为:
$$ G(v,ω)=σ(α⋅heading(v,ω)) + σ(β⋅dist(v,ω)) + σ(γ⋅velocity(v,ω)) $$其中,heading(v, ω)是方位角的评价函数,轨迹终点方向与目标终点的夹角为Δθ,用heading(v, ω) = π – Δθ作为方位角的评价函数,则夹角越小评分越高。dist(v,ω)是距离的评价函数,表示当前状态下无人船与障碍物的最小距离,距离越远越安全,评分越高。velocity(v,ω)是速度评价函数,直接用当前线速度大小作为函数值,在当前方向上的速度越快意味着轨迹越优。
α、β 、γ均为评价函数的系数,当我们对哪一部分的评分更加看重时可以通过调节评价系数来调整对轨迹的选择。σ则是对评价函数的归一化处理:
$$ \left\{ \begin{aligned} σ⋅ heading(v,ω) &=normalize\_heading(i)= \frac{heading(i)}{\sum_{i=1}^nheading(i)} \\ σ⋅dist(v,ω) &= normalize\_dist (i)= \frac{dist (i)}{\sum_{i=1}^ndist (i)} \\ σ⋅velocity(v,ω) &= normalize\_velocity (i)= \frac{velocity (i)}{\sum_{i=1}^nvelocity (i)} \end{aligned} \right. $$其中,n是采样速度空间的组合数目即轨迹数目。
经过速度采样、轨迹预测、轨迹评价后,得到当前无人船的运动仿真轨迹,如下图所示:
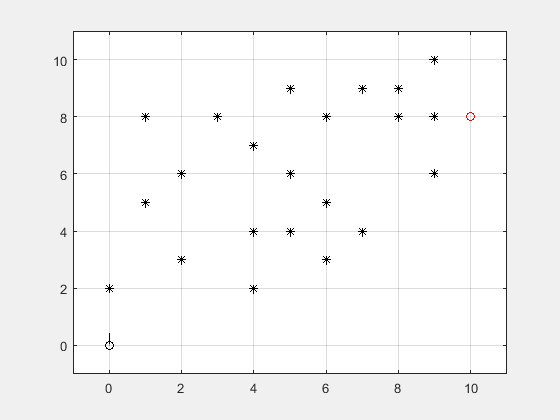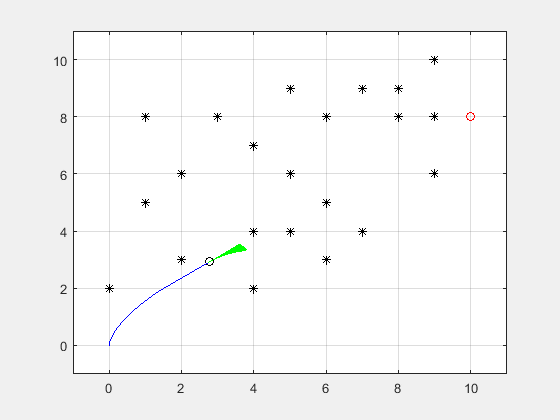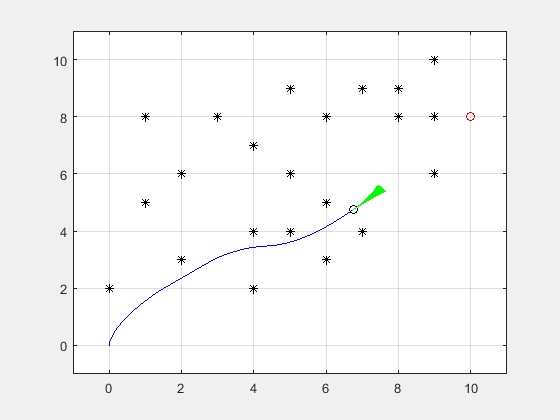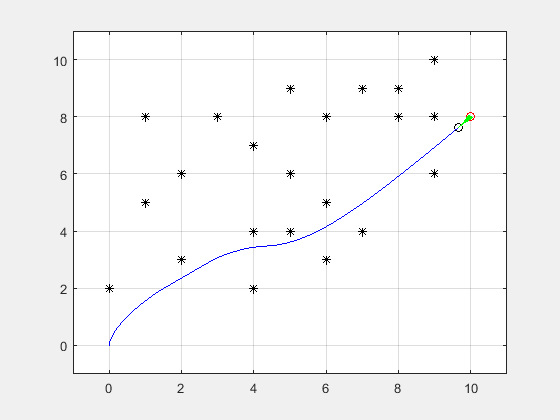
图中蓝色曲线是通过评价函数选定的最优(仅针对动态窗口算法的评价标准)路径,绿色区域是由n条待评价轨迹组合成的,表示无人船可能的轨迹。







