本文是一篇综述，从路径搜索和轨迹优化这两个层面来对目前的路径规划算法进行总结。

路径搜索

Astar*

文章提到了两种Astar的改进算法：一种稀疏Astar算法，对转角的最大增量做了限制，得到的曲线更加平滑；一种结合自适应替换缓存（ARC）策略与基于Astar算法的Theta star算法——Angular rate-constrained path planning algorithm for unmanned surface vehicles，考虑了角速度约束得到了更符合其运动特性的规划路径（我认为比较符合我们的需求）

另外除了海域内的障碍，还需要考虑到船只，以及船舶安全领域、国际海上避碰规则等真实因素限制。

虚拟势场法

包含人工势场法和快速行进法

人工势场法*

人工势场APF借鉴了电势场的概念，目标点产生引力，而障碍物产生斥力，引力场与斥力场叠加形成包含引导USV到达目标点及避障信息的人工势场。传统APF针对动态避障效果较差，集群运动需要考虑到船舶之间的距离。

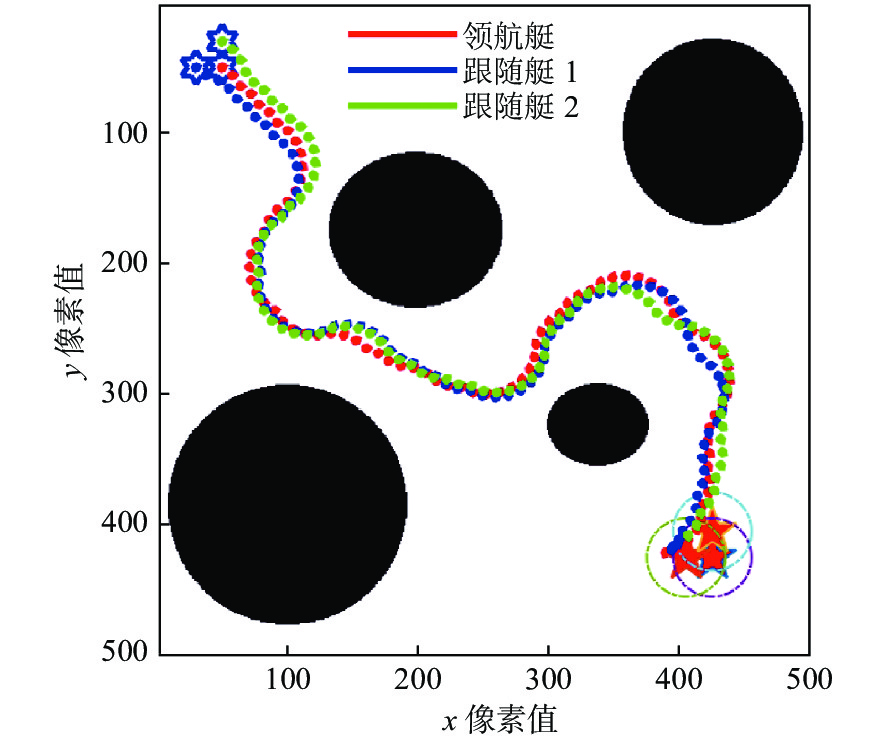
The hybrid path planning algorithm based on improved A* and artificial potential field for unmanned surface vehicle formations这篇论文中提出的改进APF方法，在结合Astar算法的前提下，对集群编队采用了优先策略，设置一个领队，一个跟随者，一个副跟随者。通过检测船舶之间的距离对速度进行控制来避免集群之间碰撞：跟随者与副跟随者距离靠近时，副跟随者减速，反之加速。形成队形后再按照Astar规划的路径前行。

快速进行法

$|∇(T(s))|W(s)=1$

利用二值栅格法进行环境建模，将障碍物区域设为$W(i, j)=0$，将可通行区域设为。$W(i, j)=1$通过数值求解程函方程，得到地图中各网格点的T值，将其视为势场值，从而建立虚拟势场

与APF法相比，FMM法构建势场唯一的极小值点便是起点，不存在路径陷入局部极小值问题（暂时不考虑）

智能算法

遗传算法

GA算法的实时性较差，一般不用于实时规划，用于离线规划，暂不考虑

粒子群算法

通过最优解的位置启发其它粒子朝着最优解方向前进，从而实现粒子群整体朝着最优解的方向收敛，本文中提到的算法年代久远了需要重新调研

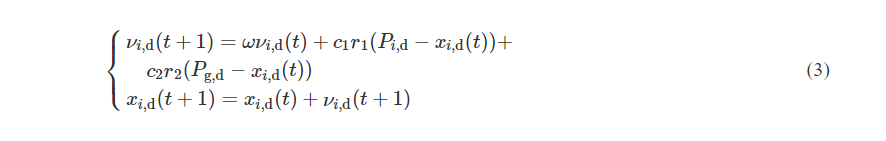
$v_{i,d}$为当前代数下粒子运动速度；$x_{i,d}$为当前代数下粒子位置；$P_{i,d}$为当前代数下的最优解；$P_{g,d}$为历史（全局）最优解；$ω$为惯性权重；$c_1$和$c_2$为学习因子；$r_1$和$r_2$为[0 1]区间内的随机小数；t为当前迭代数。PSO算法首先初始化一群随机粒子，再通过上式进行迭代和进化，从而找到最优解

TODO 这篇文章提到的智能算法感觉不是很满意，暂时跳过，后续调研寻找新的算法补充上来

轨迹优化

Dubins

直线与圆弧组合的曲线，简便易行、计算量小；曲率变化不连续，在直线段与圆弧段的交点处曲率发生突变

Reeds-Shepp

针对可以倒退的模型可以规划出更短的路径

三次样条曲线

把区间[a,b]分成n个区间，每个小区间的曲线是一个三次方程，路径连续平滑，适合用于优化折线路径

贝塞尔曲线

由起点，终点，控制点组成，调整控制点，贝塞尔曲线的形状会发生变化。计算速度和曲线形状控制方面优于三次样条曲线

总结

只是初步的调研，目标是寻找一个能够考虑到物理约束（最大角速度）的算法，或者对给出的路径进行较好的轨迹优化